--- title: Ideal Stirling Cycle Calculator description: "Calculator Inputs Hot end temperature (K): Cold end temperature (K): Compression Ratio: Specific gas constant of working fluid (J/kg-K): Pressure at state 1 (kPa):" --- - [Employment](https://www.mide.com/mide-employment?hsLang=en) - [News](https://www.mide.com/news?hsLang=en) - [Events](https://blog.mide.com/news-events?hsLang=en) - [About](https://www.mide.com/about-mide?hsLang=en) - [Corporate Social Responsibility](https://www.mide.com/mide-corporate-social-responsibility?hsLang=en) - [About](https://www.mide.com/about-mide?hsLang=en) - [Blog](https://blog.mide.com?hsLang=en) - [ISO Certifications](https://www.mide.com/mide-iso-certifications?hsLang=en) - 1 (781)306-0609 - [**](http://www.facebook.com/MideTechnology?sk=wall) - [**](http://www.youtube.com/playlist?list=PL3GP-tuxnkvrs6GyhWD4M4MDSC390MEDc) - [**](https://www.linkedin.com/company/mide-technology-corporation) - [ISO 9001:2008](https://www.mide.com/hubfs/homepage-banner/mide-iso-14664_021925.pdf?hsLang=en) - 1 (781)306-0609   [![Mide | Hutchinson](https://www.mide.com/hubfs/Logos/hutchinson-mide-color-white-web.svg "Mide Technology")](https://www.mide.com/?hsLang=en) # Ideal Stirling Cycle Calculator ## Calculator Inputs | Hot end temperature (K): | | | --- | --- | | Cold end temperature (K): | | | Compression Ratio: | | | Specific gas constant of working fluid (J/kg-K): | | | Pressure at state 1 (kPa): | | | Volume at state 1 (cc): | | | Amount of heat applied to engine (W): | | | | | ## Calculator Outputs ** ** | Predicted Frequency (RPM) | | | --- | --- | | Predicted Power Out (W) | | | Predicted Efficiency (0-1) | | | Predicted Average Pressure (kPa) | | | Swept Volume (cc) | | | Mass of Working Fluid (mg) | | | Work Out Per Cycle (J) | | | Predicted Specific Work Out Per Cycle (J/mg-working fluid) | | | Volume at State 1 (cc) | | | Absolute Pressure at State 1 (kPa) | | | Temperature at State 1 (K) | | | Volume at State 2 (cc) | | | Absolute Pressure at State 2 (kPa) | | | Temperature at State 2 (K) | | | Volume at State 3 (cc) | | | Absolute Pressure at State 3 (kPa) | | | Temperature at State 3 (K) | | | Volume at State 4 (cc) | | | Absolute Pressure at State 4 (kPa) | | | Temperature at State 4 (K) | | ## Calculated Plots --- # Summary of Equations ![Pressure vs. volume plot for the Stirling cycle](https://www.mide.com/hs-fs/hubfs/Blog-Images/Engineering/BISCEP/PV_Plot_Only.jpg?width=500&name=PV_Plot_Only.jpg "Pressure vs. 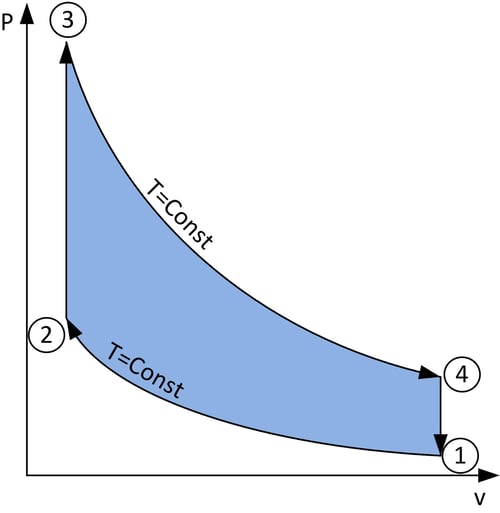volume plot for the Stirling cycle") Figure: A loop showing the relation between pressure and volume during a cycle of the Stirling engine, and with each state labelled It’s possible to calculate the fluid properties at all these different states with the following formulas: ![Summary of state equations for the Stirling cycle](https://www.mide.com/hubfs/Blog-Images/Engineering/BISCEP/Summary_Of_Equations.jpg "Summary of state equations for the Stirling cycle") Additionally, useful work produced can be calculated with the following formula. CR stands for “Compression Ratio” (max engine volume divided by min engine volume). Please note that this formula gives the amount of work per unit mass of working fluid per revolution of the Stirling engine. Temperatures must also be in an absolute scale (i.e. Rankine or Kalvin). 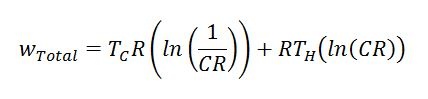![Specific work from a Stirling cycle](https://www.mide.com/hs-fs/hubfs/Blog-Images/Engineering/BISCEP/Specific_Work.jpg?width=428&name=Specific_Work.jpg "Specific work from a Stirling cycle") Equation 5: Work per unit mass of working fluid delivered by an Ideal Stirling engine per revolution (cycle) It’s important to keep in mind that all these numbers presented are for the ideal Stirling cycle, which will never exist in real life, all real engines are approximations of the ideal thermodynamic cycles. Knowing how to modify these ideal relations to reflect the real world is a whole other topic, one that might be treated in a future article! ### More Information For more information about Stirling Engines and the theory behind them, please check out the following blog posts: 1. [Thermodynamic Theory of the Ideal Stirling Engine](https://blog.mide.com/thermodynamic-theory-of-the-ideal-stirling-engine?hsLang=en) [![Mide Technology](https://www.mide.com/hubfs/Logos/hutchinson-mide-color-white-web.svg)](https://www.mide.com/?hsLang=en) **Mide Technology Corporation** 475 Wildwood Avenue Woburn, MA 01801, USA **Phone:** [+1 (781) 306-0609](tel:1781306-0609) **Email:** [Contact Us](https://www.mide.com/contact-mide?hsLang=en) [![Mide Technology](https://www.mide.com/hs-fs/hubfs/Logos/hutchinson-logos-white-hutchinson-250.png?width=180&name=hutchinson-logos-white-hutchinson-250.png)](https://www.hutchinson.com/en) *Mide is a Hutchinson Company* - [**](https://www.facebook.com/pg/MideTechnology/posts/) - [**](https://www.youtube.com/user/MideTech) - [**](https://www.linkedin.com/company/mide-technology-corporation) ##### [about](https://www.mide.com/about-mide?hsLang=en) Midé Technology Corporation, founded in 1989, is an *Innovative, Agile* and *Proven* engineering company that develops, produces and markets high performance products and solutions. Our Brands include; [Marine Seals](https://www.mide.com/mide-marine-overview?hsLang=en), [Piezo.com](https://piezo.com/) and [enDAQ.com](https://endaq.com/). Our innovative people, systems approach, and customer focus provides us with the ability to conceptualize, design and deliver these high performance, intelligent systems and services tailored to our clients’ specific needs. ##### QUICK LINKS - [Piezo Products (Piezo.com)](https://piezo.com/) - [Data Loggers (enDAQ.com)](https://endaq.com/) - [Engineering Services](https://www.mide.com/collections/capabilities?hsLang=en) - [Mide Marine Division](https://www.mide.com/collections/mide-marine-overview?hsLang=en) - [Employment](https://www.mide.com/pages/employment?hsLang=en) - [Corporate Social Responsibility](https://www.mide.com/mide-corporate-social-responsibility?hsLang=en) ### NEWS & EVENTS Mide Technology Corp. [Copyright Policy](https://www.mide.com/pages/copyright-policy-mide?hsLang=en) [Privacy Policy ](https://www.mide.com/pages/privacy-policy?hsLang=en) [ Terms & Conditions](https://www.mide.com/pages/terms-conditions?hsLang=en) [ Shipping & Ordering Policy ](https://www.mide.com/pages/shipping-and-ordering-policy?hsLang=en)